- 문제설명
- 가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다. 이 종이를 격자 선을 따라 1cm × 1cm의 정사각형으로 잘라 사용할 예정이었는데, 누군가가 이 종이를 대각선 꼭지점 2개를 잇는 방향으로 잘라 놓았습니다. 그러므로 현재 직사각형 종이는 크기가 같은 직각삼각형 2개로 나누어진 상태입니다. 새로운 종이를 구할 수 없는 상태이기 때문에, 이 종이에서 원래 종이의 가로, 세로 방향과 평행하게 1cm × 1cm로 잘라 사용할 수 있는 만큼만 사용하기로 하였습니다.
가로의 길이 W와 세로의 길이 H가 주어질 때, 사용할 수 있는 정사각형의 개수를 구하는 solution 함수를 완성해 주세요.
- 가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다. 이 종이를 격자 선을 따라 1cm × 1cm의 정사각형으로 잘라 사용할 예정이었는데, 누군가가 이 종이를 대각선 꼭지점 2개를 잇는 방향으로 잘라 놓았습니다. 그러므로 현재 직사각형 종이는 크기가 같은 직각삼각형 2개로 나누어진 상태입니다. 새로운 종이를 구할 수 없는 상태이기 때문에, 이 종이에서 원래 종이의 가로, 세로 방향과 평행하게 1cm × 1cm로 잘라 사용할 수 있는 만큼만 사용하기로 하였습니다.
- 제한사항
- W, H : 1억 이하의 자연수
- 힌트1
-
더보기대각선으로 자를 때 몇 개가 잘리는지 패턴이 있습니다.
- 힌트2
-
더보기전체에서 생각하지 말고 반복되는 작은 사각형에서 잘리는 개수를 먼저 파악해보세요.
대각선으로 이동하면서 x,y가 모두 정수인 점이 있다면 해당 패턴이 반복될 것입니다 - 힌트3
-
더보기x값을 기준으로 0~1 1~2 2~3 이런 식으로 구간 별로 대각선이 지나갈 때 사각형이 몇 개가 잘리는지 규칙을 찾아보세요.
해당 규칙을 찾을 때, 밑변이 높이보다 크게 잡아서 기울기가 1 이하가 되면 좀 더 쉬워집니다. - 해설
기본 접근은 w와 h의 최대공약수(gcd)를 이용하는 것입니다.
대각선이 0,0에서 시작해서 x,y 점이 정수가 된다면, 2x,2y에서도 다시 정수가 됩니다.
이러한 패턴은 w와 h의 gcd만큼 반복될 것입니다.
ex) 8,12의 사각형이 있다면 2,3 마다 정수 점을 지납니다.
그렇다면 w와 h를 gcd로 나눠서 그 안에서 몇 개의 사각형이 잘리는지 구한 뒤, gcd만큼 곱해주면 총 잘린 사각형의 개수가 나옵니다.
그리고 패턴이 진행되는 사각형의 크기는 w’=w/gcd, h’=h/gcd가 됩니다.
x축 구간을 1로 나눠서 해당 구역 내에서 몇 개의 사각형이 잘리는지 생각합니다.
그러면 나눈 구간의 y값에 따라 몇 개의 사각형이 잘리는지 알 수 있습니다.
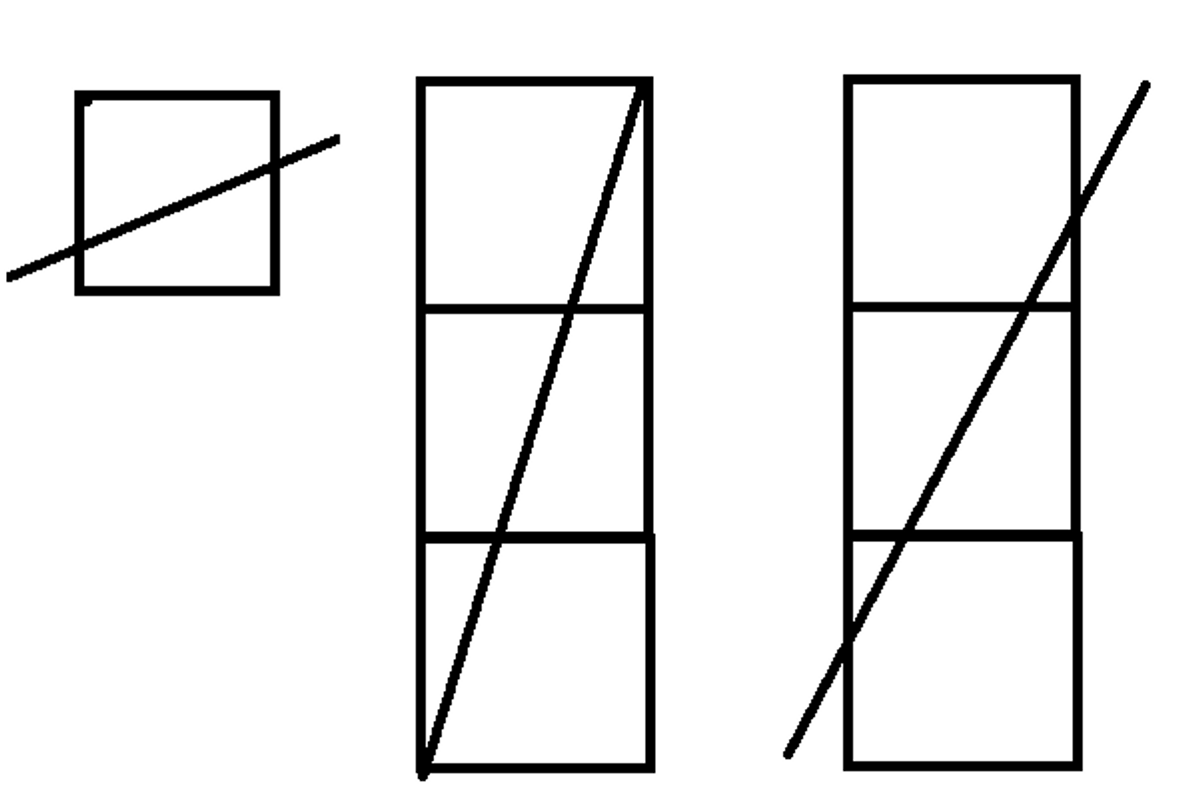
이와 같이 구간 내부에서 y축과 평행한 선과 몇 번 교차하느냐에 따라 잘리는 사각형의 개수가 일정합니다.
그러나 기울기가 1보다 클 경우 구간 내에서 몇 개가 잘릴지 구하기 까다롭습니다.
그러므로 밑변이 높이보다 크도록, w’>h’가 되도록 사각형을 돌려서 생각합니다. (결과적으로 상관은 없으나 원리를 이해하기 위해 돌려서 생각하면 쉽습니다.
이러면 기울기가 언제나 1 이하가 되므로 사각형은 구간 내에서 무조건 1 개나 2 개가 잘립니다.
이 때, 사각형이 2 개가 잘리는 경우를 생각하면
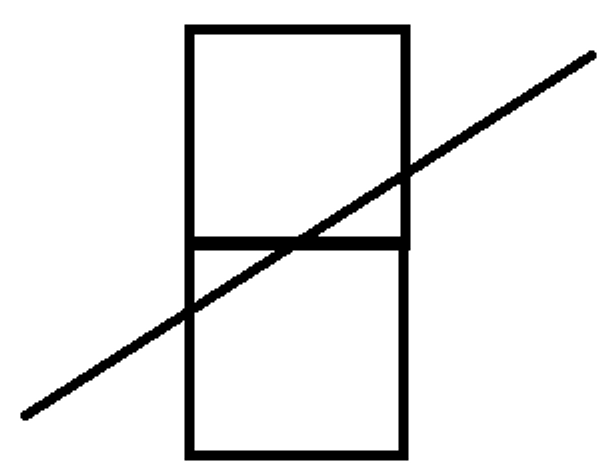
이와 같이 y축과 평행한 선과 대각선이 만날 때 밖에 없습니다.
그리고 대각선이 y축과 평행한 선과 만나는 경우는 항상 h'-1번만 일어납니다.
1개만 잘리는 경우는 w'-(h'-1)번만 일어나게 됩니다.
결과적으로, 패턴 내에서 잘리는 사각형의 개수는 (w’-h’+1) + 2*(h’-1)이므로
w’+h’-1 개가 잘립니다.
그러면 이러한 패턴이 gcd만큼 반복되므로 총 잘리는 사각형의 개수는
gcd*(w’+h’-1)이 되고 이 값을 총 사각형 개수에서 빼주면 됩니다.
answer = wh - gcd(w’+h’-1) = w*h - w - h + gcd (w’=w/gcd, h’=h/gcd)
즉, w*h - w - h + gcd가 정답이 됩니다.
'프로그래머스' 카테고리의 다른 글
| [Programmers] Lv3. 다단계 칫솔 판매 (0) | 2023.03.31 |
|---|---|
| [Programmers] 보석 쇼핑 (0) | 2023.03.24 |
| [Programmers] 큰 수 만들기 (0) | 2023.03.24 |
| [Programmers] 점프와 순간이동 (0) | 2023.03.24 |
| [Programmers]LV3. 기지국 설치 (0) | 2023.03.15 |
